Są takie odmiany piękna, których trudno doświadczyć laikowi. Takiego piękna doświadczają naukowcy, stykając się z pięknymi ideami w swojej pracy naukowej. Polscy matematycy i matematyczki mówią, że piękny dowód lub twierdzenie powinno być proste, sprytne, doniosłe, pokazywać nieoczekiwane związki między odległymi na pozór pojęciami i powinno zmieniać sposób myślenia wielu osób.

Piękny dowód lub twierdzenie powinno być proste, sprytne, doniosłe; powinno pokazywać nieoczekiwane związki między odległymi na pozór pojęciami i powinno zmieniać sposób myślenia wielu osób - powtarza się w ich komentarzach.

"Estetyka w matematyce jest bardzo ważna. To poczucie, że robi się coś na granicy tworzenia" - komentuje prof. Piotr Nowak. Tłumaczy, że piękno łatwiej w matematyce dostrzec, kiedy wejdzie się na poziom, z którego widzi się matematykę z góry, zaczyna się zauważać, że w różnych kawałkach tego obszaru wiedzy pojawiają się podobne pomysły, obiekty, wyrażone w innych językach, że jest w nich "coś uniwersalnego".

Prof. Nowak cytuje wybitnego lwowskiego matematyka Stefana Banacha: "Matematykiem dobrym jest ten, kto umie znajdować analogie między twierdzeniami, lepszym - kto widzi analogie między dowodami, jeszcze lepszym - kto dostrzega analogie między teoriami, a można wyobrazić sobie i takiego, co widzi analogie między analogiami".

Prof. Rafał Latała z kolei zaznacza: "W matematyce chyba tak jak w sztuce - piękno jest subiektywnym odczuciem. Może tylko w większym stopniu wymaga 'wyrobienia'. Choć są pewne twierdzenia (np. z teorii liczb), które za piękne uzna większość osób zajmujących się matematyką - niekoniecznie zawodowo".

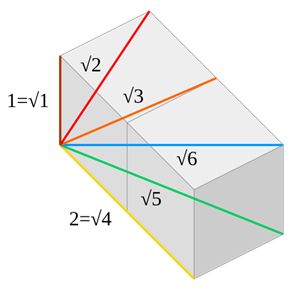
Prof. Marek Kordos, założyciel czasopisma “Delta” tłumaczy, że matematyka właściwie jako jedyna dziedzina nauki wyznaczyła bardzo restrykcyjnie dobrane metody pozyskiwania odpowiedzi na stawiane pytania i odmawia rozstrzygania większości problemów. “Ale gwarantuje pewność uzyskanych rezultatów. Tak pozyskiwana wiedza poraża, przeraża swą arystokratyczną doskonałością, separuje się od pospólstwa swą hermetyczną elitarnością. Żąda od użytkownika posługiwania się jej językiem i bezwzględnego przestrzegania jej praw. Jest zimna i piękna jak Królowa Lodu. Tak jak ona jest wszechmocna, ale też tak jak ona - przez niektórych kochana”.
 

PODOBAJĄ MI SIĘ PIOSENKI, KTÓRE JUŻ ZNAM?

Prof. Paweł Strzelecki z UW opowiada, że piękno matematyki w zaskakujący sposób ukazuje mu się czasem podczas słuchania muzyki: "Kiedy mam umysł ‘rozgrzany’ intensywną pracą nad jakimś problemem matematycznym i idę na koncert, to czasem czuję, że matematyka gra mi w głowie razem z tą muzyką. Widzę obiekty, związki między nimi. Jeśli muzyka jest odpowiednio złożona, skomplikowana, pojawiają mi się przed oczami analogie między matematyką a dźwiękami" - mówi Strzelecki.

Prof. Piotr Nowak też porównuje matematykę i muzykę. "Wiele osób ma taki album muzyczny czy piosenkę, które silnie na nich oddziałują - bo w muzyce bywa coś takiego, że aż ciarki przechodzą. Wydaje mi się, że podobne emocje pojawiają się u matematyka na myśl o pięknym dowodzie czy argumencie, do którego chce się wrócić. Jakby przesłuchiwało się od nowa ulubioną piosenkę".

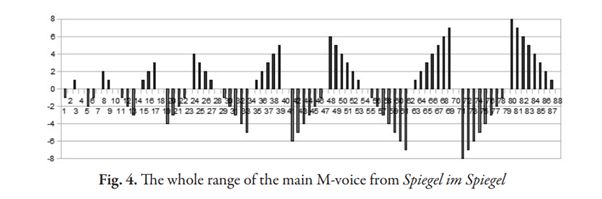
Prof. Latała z kolei komentuje: "Chyba częściej atrybut piękna przypisałbym twierdzeniom czy pewnym ideom, a nie poszczególnym dowodom. Z drugiej strony często się mówi, że jakiś dowód się bardzo podoba, a inny jest wymęczony czy brzydki. Ale piękno dowodu to już naprawdę bardzo subiektywna sprawa".

Dr Paulina Rowińska, absolwentka Imperial College London, autorka popularnonaukowej książki "Mapmatics" inaczej rozumie pojęcie piękna. "Piękna to może być według mnie muzyka. O książkach rzadko myślę, że są piękne. A twierdzenie matematyczne - to już w ogóle trudno mi postrzegać w kategoriach piękna. Według mnie wynik w matematyce może być elegancki i satysfakcjonujący... Ale jednak to nie są takie uczucia, jakie wywołuje muzyka".

EMOCJE

Jakich emocji doświadczają matematycy, zapoznając się z "elegancką" pracą badawczą? "Pewnie porównałbym je do oglądania filmu czy czytania powieści, gdy można się zachwycić sposobem prowadzenia fabuły. Trochę naciągając - przeczytanie pracy z nową, piękną metodą jest jak obejrzenie ‘Obywatela Kane’a’ po raz pierwszy" - porównuje prof. Rafał Latała.

Dr Mikołaj Frączyk, prof. Uniwersytetu Jagiellońskiego, szef centrum DIOSCURI z kolei porównuje emocje przy poznawaniu ciekawych dowodów do czytania interesującej i wciągającej książki. Jeśli jednak chodzi o doświadczanie piękna w swoich badaniach - jest trudniej. "Ciężko mi znaleźć codzienną porównywalną sytuację. Ładne rozwiązania są rzadkie, a naprawdę piękne pojawiają się raz na parę lat. Często nie wiadomo, czy 'ładny' pomysł zadziała. W większości przypadków okazuje się, że nie".

Dr Paulina Rowińska również mocno stąpa po ziemi. "Nie chciałabym romantyzować matematyki. Rozmawiałam o pięknie z moimi znajomymi matematykami: większość z nas nie doświadcza go na co dzień. Nasze badania dokładają powoli do wyników innych badaczy. Pośrednie wyniki są mało ciekawe. Kiedy patrzymy na nasze wyniki, to najczęściej nie doświadczamy tego piękna. To oczywiście zdarza się matematykom, ale w moim otoczeniu to rzadkie przypadki".

Prof. Nowak komentuje, że rzeczywiście doznawanie piękna może zależeć od obszaru matematyki - w niektórych działach łatwiej o zachwyt niż w innych. Jego zdaniem np. jego dziedzina - związana z geometrią - pozwala w miarę często stykać się z pięknem.

PIĘKNO NATURALNE CZY PIĘKNO DZIEŁ SZTUKI?

Paweł Strzelecki zwraca uwagę na jeszcze jeden aspekt związany z pięknem. "Matematycy platonicy mają przeświadczenie, że istnieje jakaś złożona struktura i oni - dzięki swoim pomysłom - ją odkrywają, tak jak odkrywano nowe lądy w czasach odkryć geograficznych. Nie wymyślają więc struktury, tylko zauważają jej istnienie”. A przy takim podejściu zachwyt bliższy jest może raczej zachwytowi nad naturą, a nie nad eleganckim dziełem człowieka.

Prof. Adam Skalski z Instytutu Matematycznego PAN tłumaczy: "Piękno to uczucie zrozumienia, dostrzeżenia czegoś nowego. Często chodzę po górach i zdarza mi się sytuacja, kiedy po całym dniu wędrówki docieram na szczyt. Widzę z niego cały szlak, którym szedłem i miejsca, które mijałem po drodze tego dnia. Zaczynam wtedy moją drogę rozumieć inaczej, bo widzę ją z innej perspektywy".

Również dr Tomasz Miller z UJ, laureat konkursu Popularyzator Nauki mówiąc o emocjach towarzyszących matematykom przywołuje metaforę wędrówki po górach “to radość, oszołomienie i zachwyt podszyte satysfakcją, że się tu wybraliśmy. No i ciekawość tego, co jest za następną granią”.

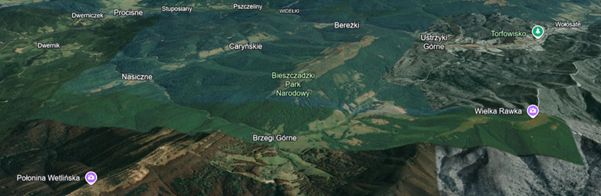
O procesie odkrywania piękna mówi też prof. Leokadia Białas-Cież z UJ. "Piękno w matematyce odkrywam, gdy badam pojęcia, które intuicyjnie wydają mi się powiązane, choć ich relacje nie są widoczne" - opowiada. Porównuje je - a im dłużej bada te pojęcia, tym lepiej je rozumie. "Układam ich własności jak fragmenty puzzli, ale wciąż nie wiem, czy te fragmenty uda się połączyć w całość i co będzie przedstawiał obraz. Czasem udaje się złożyć ze sobą ułożone wcześniej fragmenty i uzyskać klarowny, wyraźny, piękny obraz, który wiele mi tłumaczy. Obraz jest tym piękniejszy, im więcej zagadnień dotyka, im więcej pojęć ze sobą łączy, im ich relacje są łatwiejsze do wypowiedzenia, im ciekawsze są jego interpretacje".

DEFINICJE PIĘKNA

Jakie cechy powinien posiadać piękny dowód w matematyce? Mikołaj Frączyk komentuje: "Nie potrafiłbym podać definicji. To trochę tak jak z preferencjami kulinarnymi: lubię naleśniki, ale nie wiem, dlaczego". I rzeczywiście - w rozmowach z matematykami słychać, że trudno im mówić o pięknie. Oni je czują, ale trudno im zdefiniować, dlaczego.

W wypowiedziach matematyków powracają opinie, że piękne twierdzenie i rozwiązanie powinno:

A) być proste, zwięzłe, klarowne, zrozumiałe dla jak największej liczby osób, nie używać brutalnych czy nadmiarowych środków

B) być nieoczywiste, zaskakujące, wywoływać żywe emocje

C) łączyć różne punkty widzenia, pokazywać nieoczekiwane związki, znajdować zastosowanie w różnych

D) być doniosłe, dotyczyć ważnych zagadnień

PROSTOTA, ZWIĘZŁOŚĆ, NIEOCZYWISTOŚĆ

Prof. Nowak tłumaczy, że piękny dowód powinien wydać się prosty i naturalny. "Człowiek patrzy na to i myśli: dlaczego jeszcze nikt wcześniej na to nie wpadł?"

Dr Paulina Rowińska dodaje, że czasem elegancja związana jest z elementem zaskoczenia. "Do udowodnienia twierdzenia z jednego działu matematyki można użyć narzędzi z innego obszaru dziedziny. I tak, zamiast rozwiązywać jakieś równanie standardową drogą, można je rozwiązywać szybciej, bo znajdzie się drogę na skróty wiodącą przez inny dział matematyki. Np. dane zadanie można przedstawić w postaci graficznej, i wtedy od razu widać wszystkie rozwiązania. Dzięki temu z zadaniem można się uporać prościej, szybciej, pięknie. Nie jest jednak tak, że rozwiązanie przygotowane standardowym sposobem jest nieprawidłowe czy gorsze. Ono po prostu wydaje się mniej eleganckie".

Dr Tomasz Miller zwraca uwagę, że matematyczna elegancja wiąże się zwykle z oszczędnością formy przy bogactwie treści. “Wiele podstawowych pojęć współczesnej matematyki (takich jak metryka, topologia czy grupa) ma krótkie, proste definicje, a prowadzi do bardzo głębokich teorii i zaskakująco szerokich zastosowań” - komentuje.

Sprytny sposób na wizualne zademonstrowanie słuszności Twierdzenia Pitagorasa - przelewając wodę między naczyniami łatwo zrozumieć, że pole kwadratu zbudowanego na przeciwprostokątnej jest sumą kwadratów na przyprostokątnych. 

ŁĄCZENIE DZIEDZIN

Na szerokie spojrzenie na temat zwracają uwagę również inni matematycy. Ich zdaniem piękne jest czerpanie z matematyki jako całości. "Pięknem cechują się twierdzenia, które przekrawają kilka obszarów, układają się w poprzek podziału tematycznego. Stanowią połączenie między odległymi obszarami" - ocenia prof. Nowak.

Prof. Strzelecki podaje przykład Wielkiego Twierdzenia Fermata: chociaż problem dotyczył teorii liczb, to dowód Andrew Wilesa czerpał z geometrii algebraicznej a nie teorii liczb.

A Tomasz Miller podaje przykład szeregu Gregory'ego, który przerzucił jeden z pierwszych, zaskakujących pomostów między geometrią a analizą matematyczną.

DONIOSŁOŚĆ

Prof. Paweł Strzelecki zwraca uwagę na to, że piękny dowód powinien dotyczyć doniosłej tematyki. "Doniosłe jest coś, czego nie umiało zrobić wiele innych osób, przez długi czas. Jakaś zwykła łamigłówka ze sprytnym rozwiązaniem jeszcze nie będzie czymś pięknym, doniosłym, co zmieni sposób myślenia ludzi i pomoże im rozwiązać inne problemy".

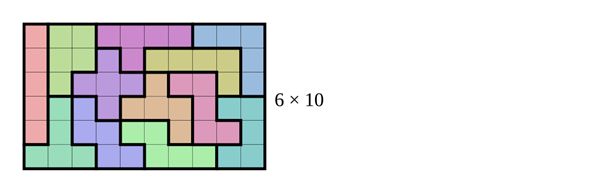
"Matematyka to wielka rzeka, która meandruje, ma liczne zakola, starorzecza, odnogi, ale płynie naprzód. Są badania, które są blisko głównego nurtu i pomagają rzece płynąć; są takie, które zmieniają stronę, w którą płynie rzeka, łączą nurty. A są i zakola, wysychające odnogi, płycizny. Bez nich rzeka sobie poradzi" - porównuje Strzelecki.

I dodaje: doniosłe jest to, co zmienia sposób myślenia innych ludzi. "Strumień wiedzy płynie przez nas, pozostawiając po sobie ślady lub nie. Rolą autora jest zmieniać sposób myślenia innych ludzi. Im bardziej doniosłe są badania, tym szybciej i głębiej zmieni się sposób myślenia innych ludzi na jakiś temat. Badania poprawne, ale mniejszej wagi, nie będą zmieniały myślenia ludzi" - ocenia.

Do metafory rzeki odnosi się również Piotr Nowak. Powołuje się na Raula Botta, według którego uprawianie matematyki powinno być jak wiosłowanie w kajaku w dół rzeki: naturalne i bezwysiłkowe. "Jak człowiek za bardzo pracuje, to może to znak, że płynie pod prąd" - a to akurat w tym przypadku niezbyt korzystne.

PRZYKŁADY PIĘKNYCH IDEI

Naukowcy podają konkretne przykłady tego, co uznają w matematyce za piękne. "Przykładem takiej pięknej idei są dla mnie np. powierzchnie minimalne - uważa Mikołaj Frączyk. - W codziennym życiu możemy je zobaczyć pod postacią baniek mydlanych. Ich definicja jest umotywowana fizycznie, ale znalazły wiele zastosowań w topologii i algebrze a w przyszłości prawdopodobnie przydadzą się w Computer Science. Te 'niespodziewane' zastosowania na pewno dodają im uroku" - opowiada.

Prof. Latała podaje za to przykład Twierdzenia Green-Tao z 2004 r. Zakłada ono, że istnieją złożone z liczb pierwszych dowolnie długie ciągi arytmetyczne (liczby są tam od siebie oddalone o taką samą liczbę). "Sformułowanie jest proste, dotyczy podstawowych własności liczb naturalnych, a jednocześnie bardzo trudne do wykazania" - tłumaczy prof. Latała. Dodaje, że bardzo trudno znaleźć nawet krótki taki ciąg. A najdłuższy znany ciąg arytmetyczny z samych liczb pierwszych ma długość 27.

Innym przykładem pięknej idei matematycznej, który podaje prof. Latała, jest Teoria Galois. "Samą teorię nie tak łatwo zrozumieć (wymaga znajomości przynajmniej podstaw teorii ciał), ale jej konsekwencje - już tak" - mówi. Tłumaczy, że związana jest z nią choćby niewykonalność konstrukcji trysekcji kąta czy kwadratury koła.

Z kolei prof. Nowak podaje klasyczne twierdzenie Atiyaha-Singera. "Ono przekrawa się przez analizę matematyczną i topologię. Panowie wzięli sobie z tych obszarów dokładnie to, co było im potrzebne. I wiedzieli, gdzie tego szukać" - komentuje prof. Nowak.

Prof. Adam Skalski jako wyjątkowo piękną podaje za to hipotezę Kadisona-Singera, postawioną w 1959 roku i sformułowaną w języku teorii algebr operatorów, którą udowodniono dopiero w 2013 roku. "Dowód był naprawdę piękny: krótki, elementarny (oparty na pewnych własnościach wielomianów), a jednocześnie otwierający zupełnie nowe perspektywy - metody były proste, ale idea 'w tle' naprawdę oryginalna i możliwa do zastosowania w rozmaitych kontekstach" - mówi.

Nauka w Polsce, Ludwika Tomala

lt/ zan/